Овог нэр: Хүдэр Отгондорж
Албан тушаал: ХШУС, Математикийн тэнхимийн ахлах багш
Судалгааны чиглэл:
Бүтээлийн нэр: Higher order Jarrat-type iterations for solving systems of nonlinear equations
Хэвлэгдсэн сэтгүүл: Applied Mathematics and Computation, Volume 395, 15 April 2021, 125849
DOI дугаар: https://doi.org/10.1016/j.amc.2020.125849
Үзүүлэлт: IF- 4.091, Cite Score- 6.8
Судалгааны бүтээлийн товч танилцуулга
 Higher order Jarrat-type iterations for solving systems of nonlinear equations
Higher order Jarrat-type iterations for solving systems of nonlinear equations
Шугаман биш тэгшитгэл ба шугаман биш тэгшитгэлийн системийг бодох өндөр эрэмбийн итерацийн аргуудыг байгуулах нь тооцон бодох математик болон шинжлэх ухаан, инженерийн хэрэглээнд чухал ач холбогдолтой. Шугаман биш тэгшитгэл, түүний системийн шийд нь аналитик байдлаар олдох нь маш ховор учраас шийдийг ямарваа аргаар ойролцоогоор олох асуудал тавигддаг.
Энэ хүү өгүүлэлд бид шугаман биш тэгшитгэлийн систем бодох Жарратын төрлийн 5 ба 6 дугаар эрэмбийн нийлэлттэй шинэ дараах аргуудыг танилцуулсан.
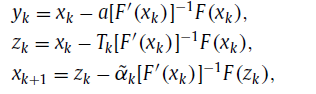
Тухайн аргуудын хувьд параметр Tk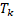 матрицын дөрвөн оновчтой сонголтуудыг дэвшүүлсэн. Шинэ аргуудын давуу тал нь:
матрицын дөрвөн оновчтой сонголтуудыг дэвшүүлсэн. Шинэ аргуудын давуу тал нь:
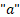 параметрийн дурын тэгээс ялгаатай утгад ажилладаг бол өмнөх судлаачдын дэвшүүлсэн арга зөвхөн 2/3
параметрийн дурын тэгээс ялгаатай утгад ажилладаг бол өмнөх судлаачдын дэвшүүлсэн арга зөвхөн 2/3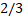 , 1/2
, 1/2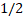 утгуудад ажиллана.
утгуудад ажиллана.
Улмаар аргуудыг практикт хэрэглэх алгоритмуудыг хийж өгсөн. Уг алгоритмуудыг ашиглан дараах тухайн уламжлалт дифференциал тэгшитгэлийн тоон шийдийг тооцоолсон.

Энэ тэгшитгэлийн шийдийг дараах ялгаварт схемүүдээр тооцоолох бөгөөд
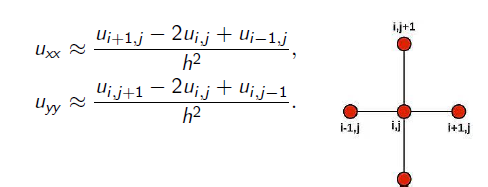
үүссэн шугаман биш тэгшитгэлийн системийг шийдэхэд MATLAB, MAPLE, MATHEMATICA зэрэг программууд дээр туршсан бөгөөд шинэ аргууд хамгийн бага хугацаа зарцуулдаг болохыг дараах хүснэгтээс харж болно.